One Of The Best Info About How To Calculate Resistors In Parallel
Parallel Resistors Diagram And Formulas Stock Vector Adobe
Understanding Parallel Resistors
1. Why Parallel Resistors Matter
Ever wondered how electronic devices manage to do so much with seemingly so little? Resistors play a HUGE role, and when they're connected in parallel, things get even more interesting. Think of it like this: a single lane road can only handle so much traffic, but add another lane running alongside it, and suddenly, you've doubled your traffic capacity! That's kind of what parallel resistors do for electrical current. They provide multiple paths for the current to flow, making it easier and more efficient.
Unlike resistors in series (where the current has to go through each resistor, one after the other), resistors in parallel offer alternative routes. This lowers the overall resistance of the circuit. Its like having multiple checkout lanes open at the grocery store everyone gets through faster!
So, why would you want lower resistance? Well, sometimes you need to limit the current in a specific part of a circuit. Adding resistors in parallel allows you to achieve this without affecting other components too much. It's all about fine-tuning the flow of electricity to make things work just right. Think of it as the circulatory system of your electronics, ensuring everything gets the right amount of "blood" (electricity) to function properly.
Understanding how to calculate resistors in parallel is crucial for anyone tinkering with electronics, whether you're building a robot, fixing a broken appliance, or designing your own circuit board. Don't worry, it's not rocket science! Once you grasp the basic concepts, you'll be able to manipulate resistance with confidence and create all sorts of amazing things.
2. The Reciprocal Resistance Formula
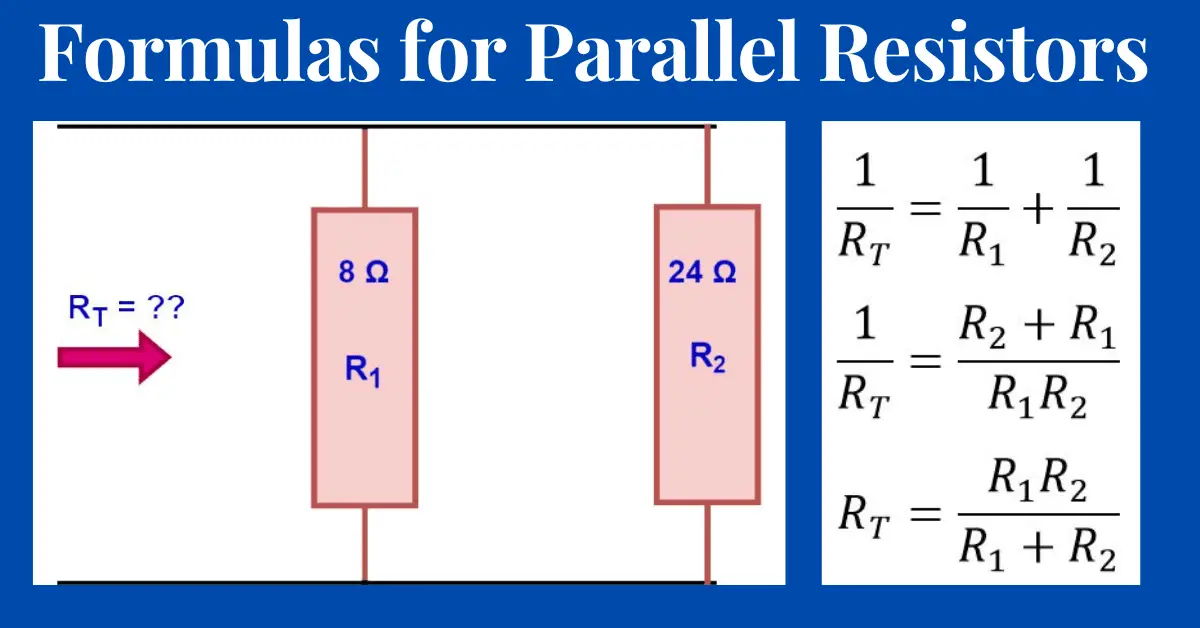
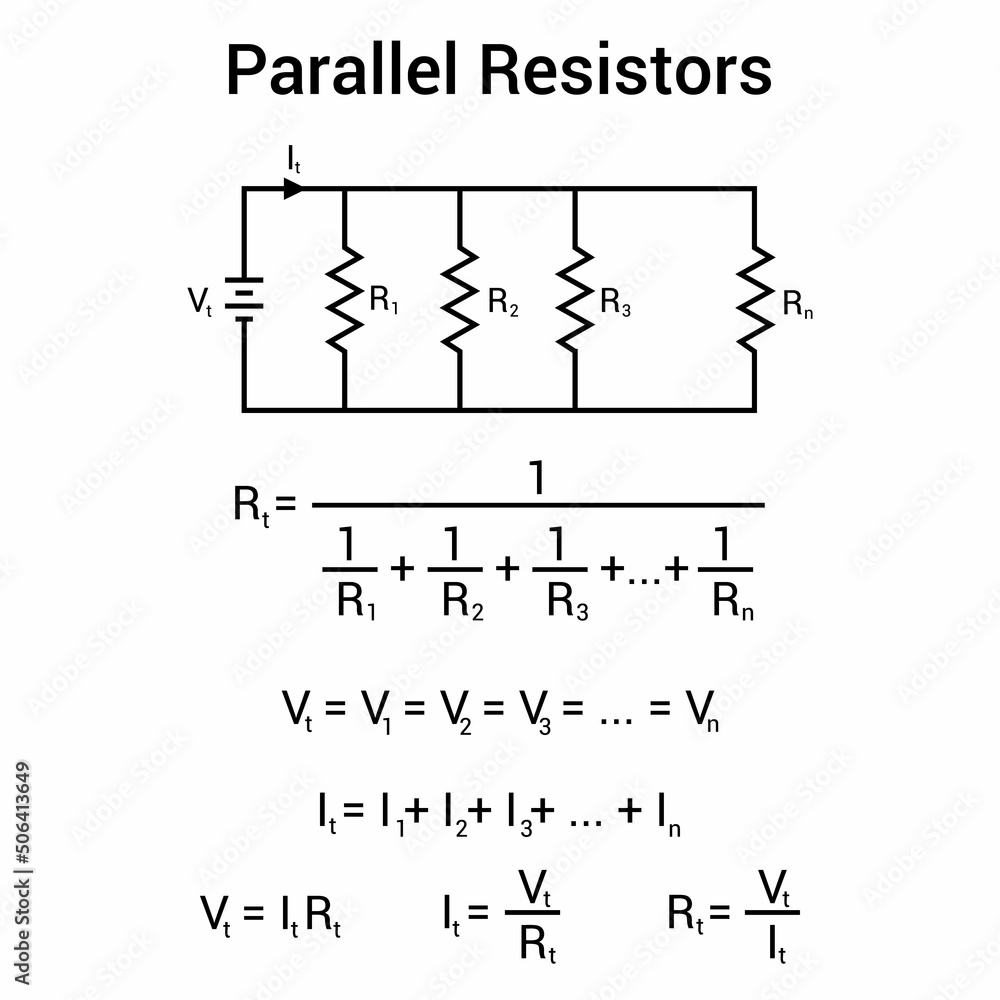
Alright, let's get to the math! The formula for calculating the total resistance of resistors in parallel might look a little intimidating at first, but trust me, it's easier than parallel parking (most of the time!). The core idea is that the reciprocal of the total resistance is equal to the sum of the reciprocals of each individual resistance. Deep breath, here it comes:
1/Rtotal = 1/R1 + 1/R2 + 1/R3 + ...
Where:Rtotal is the total resistance of the parallel circuit.R1, R2, R3, and so on, are the individual resistances of each resistor.Yeah, it's a mouthful! But lets break it down. Imagine you have two resistors, one is 2 ohms (R1) and the other is 4 ohms (R2). To find the total resistance, youd first calculate 1/2 and 1/4. Then, youd add those fractions together.
Once you have the sum of the reciprocals, you need to find the reciprocal of that sum. This final step gives you the total resistance (Rtotal). Basically, you're flipping the fraction! Now, some of you might be thinking, "Why the reciprocals? What's the point?" Well, it's all about how current flows in parallel circuits. The reciprocals allow us to account for the fact that current has multiple paths to take, and each path contributes to the overall conductivity of the circuit. Stick with it, and itll start to feel natural.

Putting the Formula to Work
3. Example 1
Let's say you have two resistors in parallel: a 10-ohm resistor (R1 = 10 ) and a 20-ohm resistor (R2 = 20 ). To find the total resistance, you would use the formula: 1/Rtotal = 1/10 + 1/20. First, find a common denominator (20 in this case): 1/Rtotal = 2/20 + 1/20 = 3/20. Then, take the reciprocal of 3/20 to find Rtotal: Rtotal = 20/3 6.67 .
So, the total resistance of the circuit is approximately 6.67 ohms. Notice that this is less than the resistance of either individual resistor. This is a key characteristic of parallel circuits — the total resistance is always lower than the lowest individual resistance. Imagine having two garden hoses connected to a single faucet. Each hose provides a path for the water to flow, and together, they allow for more water to flow than either hose could provide alone.
This principle is used in many electronic devices to create specific resistance values that aren't readily available as standard resistor values. By combining resistors in parallel, engineers can fine-tune the circuit to achieve the desired performance characteristics. Its like mixing different colors of paint to create the exact shade you need!
Remember to always use the same units for resistance (usually ohms) when performing these calculations. Mixing and matching units will lead to incorrect results, and nobody wants that! It's always a good idea to double-check your work to ensure you haven't made any silly mistakes. A calculator can be your best friend here, especially when dealing with more complex circuits.
4. Example 2
Now, let's kick it up a notch with three resistors in parallel: 5 ohms (R1), 10 ohms (R2), and 15 ohms (R3). Our formula is now: 1/Rtotal = 1/5 + 1/10 + 1/15. Again, we need a common denominator. In this case, 30 works nicely: 1/Rtotal = 6/30 + 3/30 + 2/30 = 11/30. Taking the reciprocal gives us Rtotal = 30/11 2.73 .
As you can see, even with the addition of more resistors, the total resistance remains lower than the smallest individual resistor (5 ohms). This demonstrates the additive effect of parallel resistors in reducing overall resistance. Think of it like this: youre adding more "channels" for the current to flow through, making it easier for the electricity to get where it needs to go.
This principle is particularly useful in circuits that require a specific low resistance value but can't achieve it with a single standard resistor. By carefully selecting and combining resistors in parallel, designers can create precise resistance values for a wide range of applications. It's all about understanding the relationship between individual resistances and the resulting total resistance.
Also, when working with multiple resistors, it's often helpful to use a spreadsheet or calculator to keep track of the calculations and avoid errors. There are also plenty of online calculators that can do the math for you, but it's always a good idea to understand the underlying principles so you can troubleshoot any issues that may arise. Knowledge is power, after all!

Resistors In Parallel
Simplifying Calculations
5. Equal Value Resistors
If you're lucky enough to have several resistors with the same resistance value connected in parallel, calculating the total resistance becomes incredibly simple. The formula is: Rtotal = R / N, where R is the resistance of each individual resistor, and N is the number of resistors. For instance, if you have four 100-ohm resistors in parallel, the total resistance is 100 / 4 = 25 ohms!
This shortcut is especially useful when you need to create a very specific resistance value quickly and easily. By using a bunch of identical resistors, you can avoid the more complex reciprocal calculations and get to your desired result in a fraction of the time. Its like having a cheat code for circuit design!
Keep in mind that this shortcut only works when all the resistors have the same value. If even one resistor has a different value, you'll need to revert to the reciprocal resistance formula. But when it applies, it's a real time-saver! So, always check if your resistors are identical before reaching for the calculator.
This method is also valuable when trying to reduce the power dissipated across a resistor. Using multiple equal valued resistors in parallel allows the current to be distributed among all of them. Each resistor handles a lower percentage of the total power, preventing individual components from overheating and failing. It's like sharing the workload among a team, making sure no one gets overburdened.
6. Two Resistors
For the specific case of two resistors in parallel, there's another handy formula you can use: Rtotal = (R1 R2) / (R1 + R2). This formula is derived from the reciprocal resistance formula, but it's often easier to remember and apply when you're only dealing with two resistors. For example, if you have a 10-ohm resistor and a 20-ohm resistor in parallel, the total resistance is (10 20) / (10 + 20) = 200 / 30 6.67 ohms.
This formula can save you a bit of time and effort compared to using the reciprocal resistance formula, especially if you don't have a calculator handy. It's a good trick to have up your sleeve when you're working on simple circuits. Think of it as a mini-shortcut within the larger topic of parallel resistor calculations.
While this formula is convenient, it's important to remember that it only applies to two resistors in parallel. If you have more than two resistors, you'll need to use the reciprocal resistance formula or combine resistors in pairs using this formula iteratively. Don't try to force it to work with more than two resistors, or you'll end up with the wrong answer!
Mastering this formula, alongside the general reciprocal resistance formula, provides a robust toolset for tackling a variety of parallel resistance problems. The more comfortable you become with these techniques, the easier it will be to analyze and design electronic circuits. Practice makes perfect!

FAQ
7. Q
A: Great question! If one resistor burns out, the circuit will still function, but the total resistance will increase. The current will then redistribute through the remaining resistor(s). Its like if one lane of a multi-lane highway closes; traffic slows down, but it still gets through.
8. Q
A: Yes, absolutely! Thats a key characteristic of parallel circuits. Adding more resistors in parallel always decreases the total resistance, providing more paths for the current to flow. The more paths, the easier it is for current to flow, which means lower resistance. The resulting combined resistance can never exceed the resistance value of any single resistor on the circuit.
9. Q
A: Yes, you can! By connecting resistors in parallel, you effectively distribute the current load across multiple components. This allows the circuit to handle more current without overloading any single resistor. It's like having multiple workers sharing a heavy load — each worker carries less weight, and the overall task is completed more efficiently.
10. Q
A: "Resistors" is a plural noun, and "in parallel" is a prepositional phrase acting as an adjective modifying "resistors". The overall term functions as a noun phrase.